Below are answer explanations to the 2nd full-length Math test released by ACT for the ACT 2025.
Other answer explanations in this series of articles:
- English Answer Explanations from ACT 2025 Practice Test
- Math Answer Explanations from ACT 2025 Practice Test (this article)
- Reading Answer Explanations from ACT 2025 Practice Test
- Science Answer Explanations from ACT 2025 Practice Test
When you’re finished reviewing this official practice ACT test, start practicing with our own 12 full-length practice ACT tests.
ACT 2025 Practice Test Math Answer Explanations
Question 1. The answer is A, 3.
We need athletes in high jump AND triple jump, but NOT long jump.
On the Venn diagram, identify the overlap of high jump and triple jump that lies outside long jump.
That region is labeled 3.
Question 2. The answer is J, 15.
Use the function definition:
.
Substitute
:
.
Compute:
.
Then
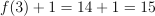 .
.
Question 3. The answer is B, −6.
Compute the sum:
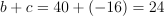 .
.The problem says this equals the product of -4 and some number k:
.
Solve:
.
Question 4. The answer is G, .
Convert 24 hours to minutes:
.
Collin walks 24 minutes, so the fraction of the day is
.
Simplify:
.
Question 5. The answer is C, 20.
Triangle angles sum to 180:
.
Combine:
.
Solve:
.
Question 6. The answer is J, .
Multiply every entry of the matrix by 6.
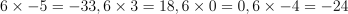 .
.So the result is
.
Question 7. The answer is A, 12.5%.
A and B are “as far apart as possible,” so AB is a diameter and arc AB is 180°.
C is halfway from A to B along the circle, so arc AC is 90°.
D is halfway from C to B, so arc CD is half of arc CB (which is 90°), so arc CD is 45°.
The region enclosed by
,
, and arc CD is a sector with central angle 45°.
Sector fraction of the circle:
.
Question 8. The answer is G, 100.9.
Model:
.
Substitute
:
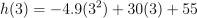 .
.Compute:
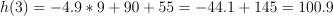 .
.
Question 9. The answer is B, (2x − 4)(2x − 3).
Factor out 2 from the first two terms:
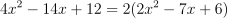 .
.Factor the trinomial:
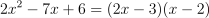 .
.Put it together:
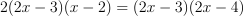 .
.Match to the choice:
.
Question 10. The answer is J, 8x + 2y.
Start:
.
Distribute the minus sign:
.
Combine like terms:
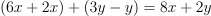 .
.
Question 11. The answer is A, 5.
Let x = number of 1-bedroom apartments and y = number of 2-bedroom apartments.
Total apartments:
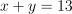 .
.Total rent:
.
Substitute
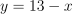 :
: 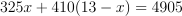 .
.Solve:
 →
→ →
.
Question 12. The answer is H, 63%.
Total customers: 312.
Customers who like hamburgers: 195.
Percent:
.
Compute:
.
Convert to percent and round:
.
Question 13. The answer is A, −21.
The quadratic is
with solutions
and
.
For a monic quadratic, the product of roots equals the constant term:
.
So
.
Question 14. The answer is J, 25.
Similar triangles scale factor (small to large) is 4:5, so multiply lengths by
.
Larger hypotenuse:
.
Question 15. The answer is B, 1/2.
For
, the amplitude is the absolute value of the coefficient in front of cosine.
Amplitude:
.
Question 16. The answer is G, (x − 3)² + (y + 4)² = 25.
Circle center is (3, -4), so equation form is
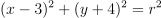 .
.Radius is distance to (0, 0):
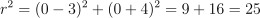
.So
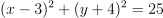 .
.
Question 17. The answer is C, 12√7.
Simplify each radical by factoring out perfect squares:
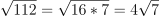 .
..
 .
.Add:
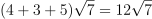
.
Question 18. The answer is G, 36.
Ratio is 5:3:2, sum of ratio parts:
.
Total sum is 180, so each “part” is
.
Integers are
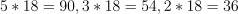 .
.Smallest is 36.
Question 19. The answer is A, 1/9.
After the first glove is chosen, there are 9 gloves left.
Exactly 1 of those 9 is the matching glove.
Probability:
.
Question 20. The answer is G, 4.
A customer gets both items when their number is a multiple of
.
Prime factorize:
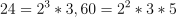 .
.LCM:
.
Multiples of 120 up to 500: 120, 240, 360, 480 → 4 customers.
Question 21. The answer is C, 67.
There are
books total.
Expected value (weighted average):
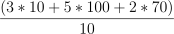 .
.Compute numerator:
.
.
Question 22. The answer is G, −17.
Sequence:
,
, and
.
.
.
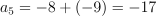 .
.
Question 23. The answer is B, y = −2.
From
, substitute into
.
.
→
.
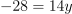 →
→ .
Question 24. The answer is J, g(x) = 2x² − 8.
Test each option using a point from the table (for example
gives
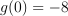 ).
).For
,
(matches).
Check another value,
:
(matches).
Since it matches multiple points, that’s the rule.
Question 25. The answer is B, 70°.
In an isosceles triangle, the two base angles are equal.
Total angle sum:
.
→
.
Question 26. The answer is H, 120°.
An equilateral triangle has all angles 60°.
The inscribed angle that intercepts arc BC is 60°.
Arc measure is twice the inscribed angle:
.
Question 27. The answer is C, 60.
The rectangle’s x-values: from -2 to 4, width
.
The rectangle’s y-values: from -3 to 7, height
.
Area:
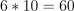 square miles.
square miles.
Question 28. The answer is F, shifted downward 4 coordinate units.
New graph is
.
Subtracting 4 from a function shifts it down 4 units.
Question 29. The answer is A, 18 tan 40°.
The 18 ft segment is adjacent to the 40° angle, and the height is opposite.
Use tangent:
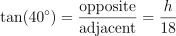 .
.Solve:
.
Question 30. The answer is J, √8 is between B and C.
is between
and
, so it’s between 2 and 3.
The segment from 0 to 8 is split into 6 equal parts, so each step is
.
Point B is at
, and point C is at
.
Since
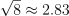 , it lies between B (≈2.67) and C (4).
, it lies between B (≈2.67) and C (4).
Question 31. The answer is B, 0.5.
Event A: wind. Event B: Deon flies.
He only flies when there is wind, so
.
He does not fly on every windy day, so
and both are ≤ 1.
must be between 0 and 1, and cannot exceed
.
0.5 is a valid probability value consistent with the statements.
Question 32. The answer is J, (6 − 3x)/(x − 3).
Factor the numerator:
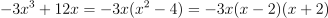 .
.Factor the denominator:
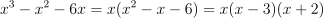 .
.Cancel common factors x and
(when defined):
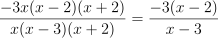 .
.Rewrite numerator:
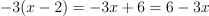 .
.Result:
.
Question 33. The answer is B, x(x − 2)(x + 5) = 0.
Roots are 0, 2, and -5.
Corresponding factors are
,
, and.
Factored equation:
.
Question 34. The answer is G, 13/19.
Start with
.
Cross-multiply:
.
Expand:
.
Combine:
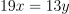 .
.So
.
Question 35. The answer is A, m1 = m2.
Put each line in slope-intercept form.
→
→
, so
.
→
→
, so
.
Therefore
.
Question 36. The answer is G, −7.
Evaluate
. Since -1 is in the first case, .
.Now evaluate
. Since
, use the second case:
.
Therefore
.
Question 37. The answer is B, (1 1/2, 13).
Intersections satisfy
:
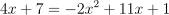 .
.Move all terms to one side:
.
Multiply by
.
Factor:
.
So
or
.
Compute y using
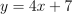 . For
. For ,
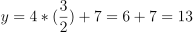 .
.The listed matching point is
.
Question 38. The answer is H, 2.4.
Compute the mean using a weighted average:
Total cities toured:
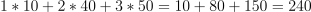 .
.Total tourists: 100.
Mean:
.
Question 39. The answer is D, 33 + 56i.
Square:
.
Use
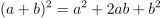 :
: .
.Compute:
.
Since
, this is
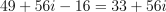 .
.
Question 40. The answer is F, Both x and y are rational.
If x and y are rational, then xy must be rational.
The problem says xy is an irrational real number.
Therefore “both rational” cannot be true.
Question 41. The answer is A, ln 4.
Solve
.
Divide by 3:
.
Take natural log:
.
Question 42. The answer is J, 5π.
In the diagram, segment BC goes through the center 0, so BC is a diameter.
An angle subtending a diameter is a right angle, so
.
The triangle is right isosceles, so the other two angles are
each.
Angle
is
and intercepts arc AB.
An inscribed angle is half its intercepted arc, so arc AB has measure
.
Arc length:
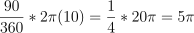 .
.
Question 43. The answer is A, y = x/2.
Speed = distance / time.
To work: speed is
.
Home: speed is
.
Given home speed is 2 times work speed:
.
Cancel d:
.
Solve:
.
Question 44. The answer is F, x²/9 + y²/36 = 1.
Hyperbola 1:
has vertices at
.
Hyperbola 2:
has vertices at
.
An ellipse that intersects all 4 of these vertices must pass through
and
.
Standard ellipse centered at origin:
.
To hit
, need
. To hit
, need
.
Equation:
.
Question 45. The answer is C, x³/2 + 1/2.
Given
.
Let
.
Cube both sides:
.
Solve for x:
→
.
Swap variables to write the inverse:
.


