
Rational numbers are numbers that can be represented as a fraction whose numerator and denominator are both integers.
Fractions Overview
The numerator is located in the top portion of a fraction, and the denominator is located in the bottom portion of a fraction. The denominator cannot be zero, as any number divided by zero is considered undefined, but the numerator may be zero. An improper fraction contains a numerator that is larger than the denominator, and a mixed number contains a fraction paired with an integer.
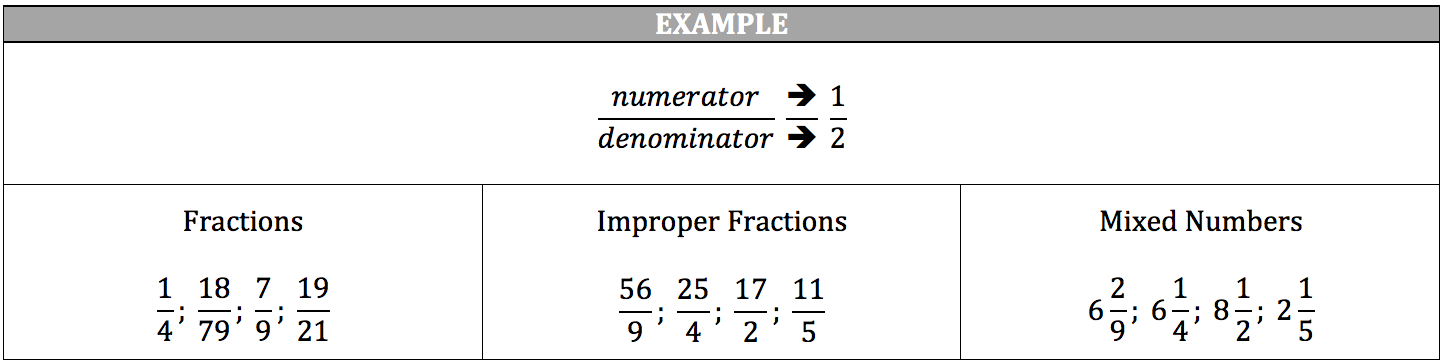
Reducing Fractions
You can also find which fraction is greater using this method as well. Since the denominator will be the same in both numbers, simply multiply one fraction’s denominator to the other fraction’s numerator. The results will let you know which fraction is greater.
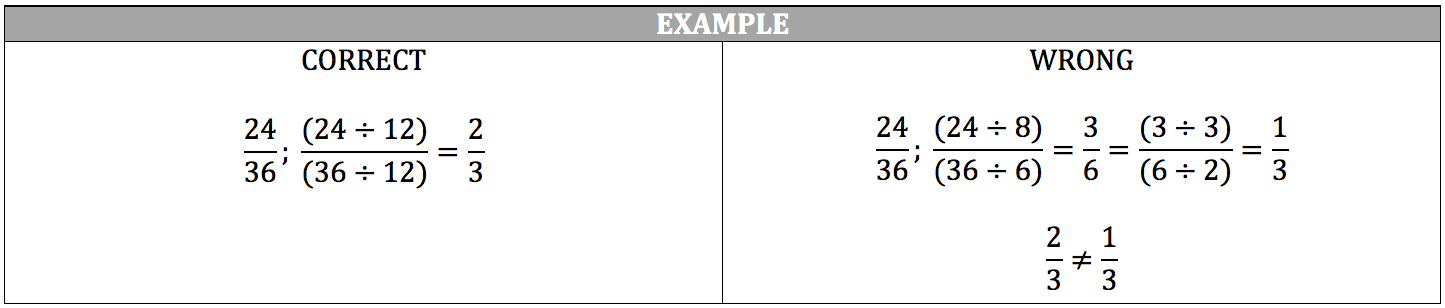
Adding and Subtracting Fractions
If you want to add or subtract fractions, all of the fractions must share a common denominator (a number that each fraction’s denominator can be a factor of). The simplest method of finding the common denominator is multiplying the denominators together. Remember, you must perform the same action to the numerator that you perform to the denominator.

Determining the Greatest Fraction
You can also find which fraction is greater using this common denominator as well. Since the denominator will be the same in both numbers, simply multiply one fraction’s denominator to the other fraction’s numerator. The results will let you know which fraction is greater.

Multiplying Fractions
For multiplication, you simply multiply across.
- The product’s numerator will be the product of the factors’ numerators.
- The product’s denominator will be the product of the factors’ denominators.
To eliminate the sheer amount of reducing you may have to perform with some fractions, you can simplify before you multiply. Multiplication is commutative, which means that the order of the integers in a multiplication problem does not matter.

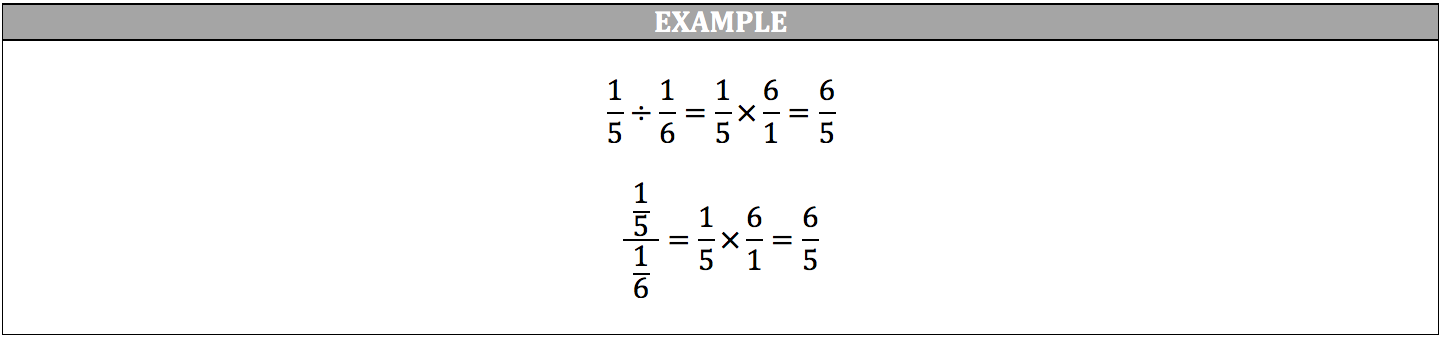
Dividing Fractions
To divide fractions, you simply find the reciprocal of the divisor (usually the second number) and multiply it to the dividend (usually the first number).
Multiplying Decimals
While addition and subtraction of decimals are a game of lining up the place values, multiplying and dividing decimals involve a little more work.
For multiplication, you multiply the values with decimals just as you would regular integers without worrying about the decimal place values.
However, the product from multiplying the values this way is not the correct answer. You must still move the result’s decimal place to the left the same number of times as the total number of decimal places contained in all of the multiplied values with decimals. An easy way to do this is count how many total decimal places there are in the values, mark the amount to the side of the values (ex. 4 dcp.), and then multiply the values.

Dividing Decimals
To divide decimals, you are still moving the decimal place. However, the movement occurs before you divide.
- Set up the values in long division, with the dividend underneath the long division symbol and the divisor to the left of the long division symbol.
- Move the decimal place of the divisor to the right until it just to the right of the last digit.
- Move the decimal place of the dividend to the right the same number of times you moved the divisor’s decimal place.
- Perform long division on the new values to achieve the correct answer.

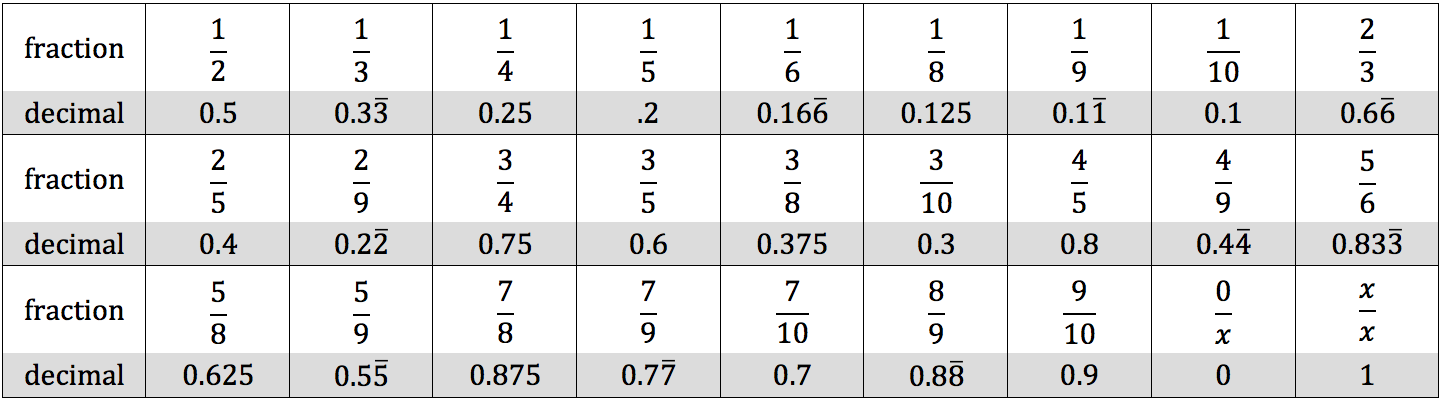
Common Fractions and Decimal Equivalents
Review these fractions and their decimal equivalents to save time on calculations (remember the ISEE does not allow calculators):



Leave A Comment