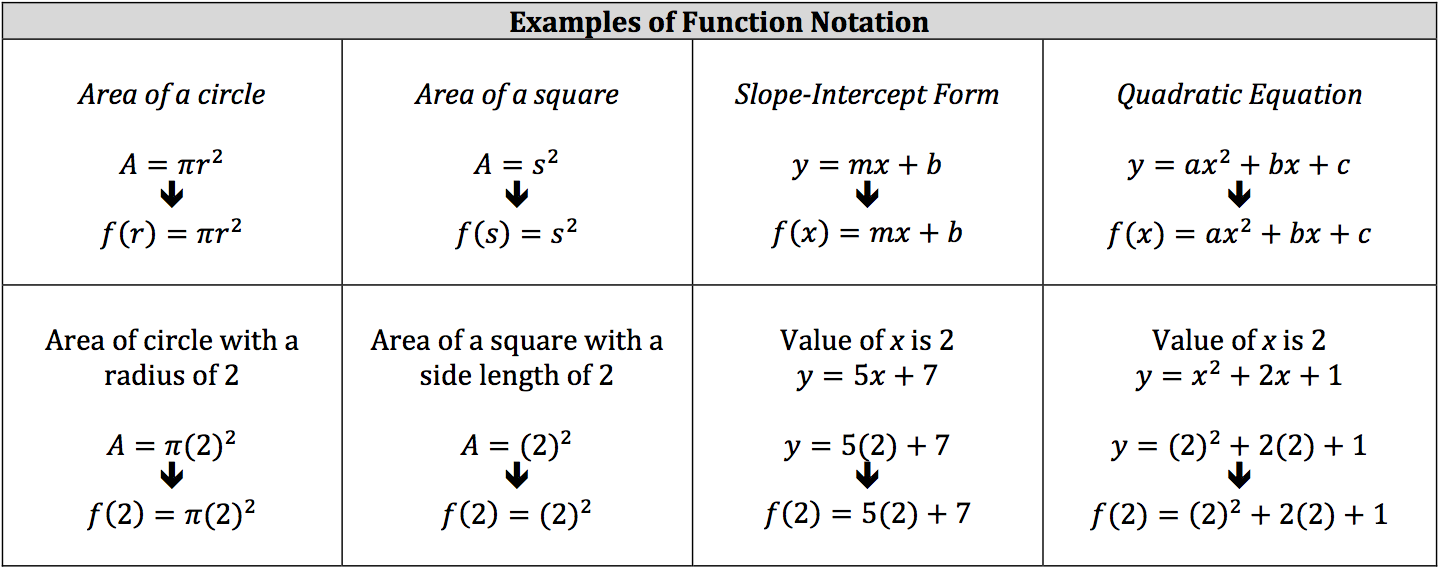
With so many formulas and equations to know and use, computations can become confusing when you must use several formulas and/or equations for the same problem. Function notation was developed to help differentiate between distinct equations and formulas, which are all considered functions.
A function is a correspondence, or relation, between two sets of data where each input (one set of data) is associated with one output (second set of data). In other words, inputting a specific value into an equation or formula will result in one specific value. If an input results in more than one output, the equation or formula cannot be considered a function.
Function notation refers to switching out the output’s variable (usually y) with a different notation: f (x). This notation is not f multiplied to x, but is simply read as “f of x.” The f is a label or a way to distinguish which equation is which. You can use whatever letter you want for function notation, but many functions will be paired with the f. The variable inside of the parenthesis is the input.




Leave A Comment