
The Upper Level ISEE is used for application into 9th through 12th grade. Thus, the ISEE sometimes includes some higher level math concepts designed for students who have completed Algebra II or Pre‐Calculus.
We have included three of these concepts so that you know what they look like so you can determine for yourself whether or not you should spend any time trying to solve them. While it is good to be prepared for everything the ISEE can throw at you, it is also prudent to focus more on the concepts that you know and can understand.
Matrix Multiplication
Matrix multiplication is the confusing process of multiplying matrices that must have certain structures. If the number of rows in the first matrix matches the number of columns in the second matrix, then everything is good to go. If they don’t, you can’t multiply them at all.

Standard Deviation
Standard deviation is part of statistics and studies how data deviates or changes from the data’s mean (average). Basically, it looks how the data spreads out in increments from the mean.

Trigonometry
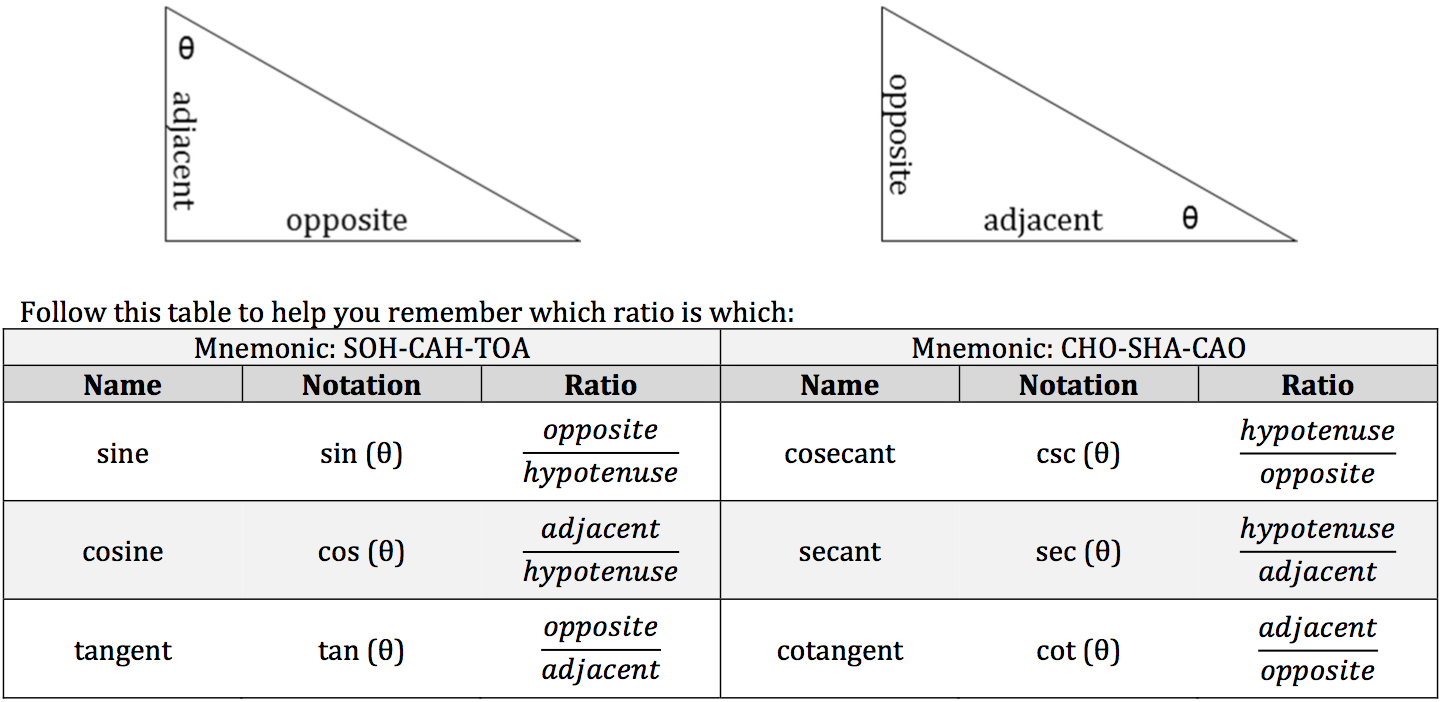
You will only need to know the very basics of Trigonometry for the ISEE, and there may only be one or two questions concerning this branch of math. However, in order to answer these questions, you need to understand sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot) in the context of right triangles. Two right triangles that have the same non‐right angles, such as two 45° – 45° – 90° triangles, will have proportional corresponding sides. For example, the ratio of one triangle’s hypotenuse to its height will be the same in the other triangle. These concepts represent these ratios.
You begin with a known non‐right angle, which is usually labeled as θ (theta). If both non‐right angles are known, then they might be labeled as α (alpha) and β (beta). From the known angle, you determine which leg is opposite from the angle and which leg is adjacent to the angle. The hypotenuse is always the slanted side.



Leave A Comment